Sorting Network IP Generator
Explanation
The Spiral Sorting Network IP Generator automatically generates customized sorting networks in synthesizable RTL Verilog. The generator is powered by our formula-driven hardware compilation tool. The networks can be latency or throughput optimized.
Sorting networks operate in parallel over the input elements, processing them through a network of comparison-exchange elements. After every comparison-exchange stage elements are permuted such that a sorted sequence is obtained at the final stage.
Sorting networks offer great performance and are particularly attractive for hardware implementations due to their inherent parallelism and input-independent structure. However, this solution becomes prohibitively expensive for large data sets because of the area cost or since elements can no longer be provided at the same time. We introduce sorting networks that can offer a variable streaming width, while maintaining high throughput capabilities. This approach dramatically reduces the footprint of sorting networks by effectively reusing hardware components to operate sequentially over the input elements.
We introduce a small domain-specific language (DSL) to represent sorting networks, borrowing concepts from [2] and [3] and using the streaming permutations from [6]. The elements of the language are structured operators (viewed as data flow graphs) that map vectors to vectors of the same length. Our DSL is designed to represent sorting networks with a regular structure, specifically those based on bitonic sorting [4][5, pp. 230].
A selection of five different sorting network architectures, derived from the original definition of bitonic sorting [4], is given to the user. The figure below shows an example one of one of these architectures (SN3) applied to an input set of 8 samples, and how every stage is represented in our DSL.
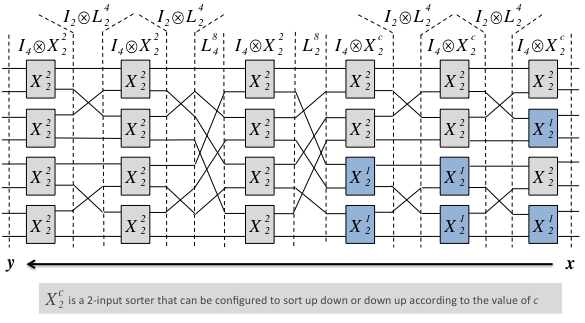
In addition to the sorting network architecture, the user has control over a variety of parameters that control the functionality and cost/performance tradeoffs such as area and throughput. Each architecture exposes different tradeoff when combined with different configurations of the implementation parameters. A short explanation of each architecture is given by clicking (?) in the architecture field of the form below. For more information, please see [1] and other related previous work in [2,3,6,7].
Our complete tool flow has considerably more flexibility than the web version presented here. In particular, we have constrained iterative reuse options to maximum reuse and minimum reuse in order to simplify the user interface. Generated sorting networks are configured to sort in down-up order. If you have an application that could benefit from our work, please feel free to contact us at the address given at the bottom of this page.
See also: online generator for DFT/FFT IP cores.
Generator
- Select problem specification parameters: input set size and data type.
- Select parameters controlling implementation in order to balance the performance and cost of the desired implementation: architecture, streaming width, iterative reuse, and BRAM budget.
- Click "Generate Verilog." A window will appear that includes: performance information (throughput and latency, in cycles); resource consumption (number of memories); and a link to your synthesizable register-transfer Verilog description. Additionally, the Verilog file will include a small example test bench to demonstrate the timing and control signals.
Please select parameters in order (from top to bottom), as the parameters chosen may restrict the choices below. For more information about any parameter, please click on (?) in the explanation column.
Benchmarks
The design space of solutions generated by the available algorithmic and implementation choices has been evaluated and compared against other sorting algorithms for hardware. BRAM budget was only evaluated with configurations 0 (no BRAMs) and -1 (no limit). All designs are synthesized using Xilinx ISE, and all cost and performance data are collected after place and route.
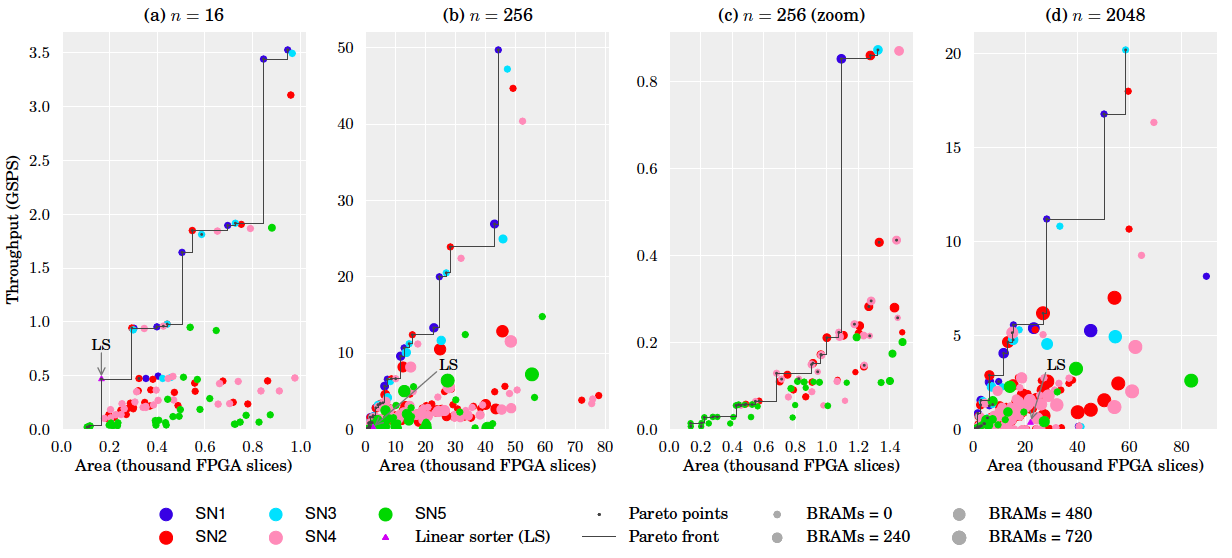
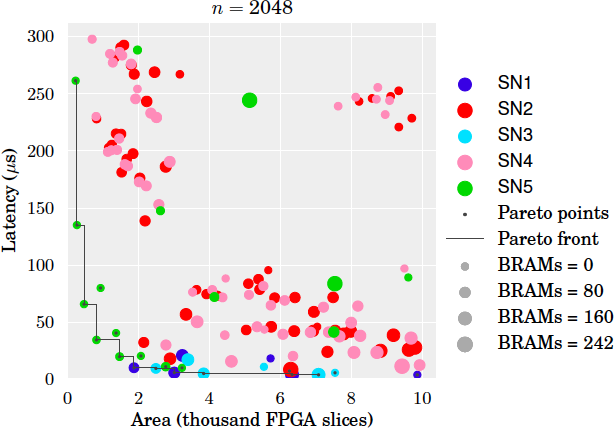
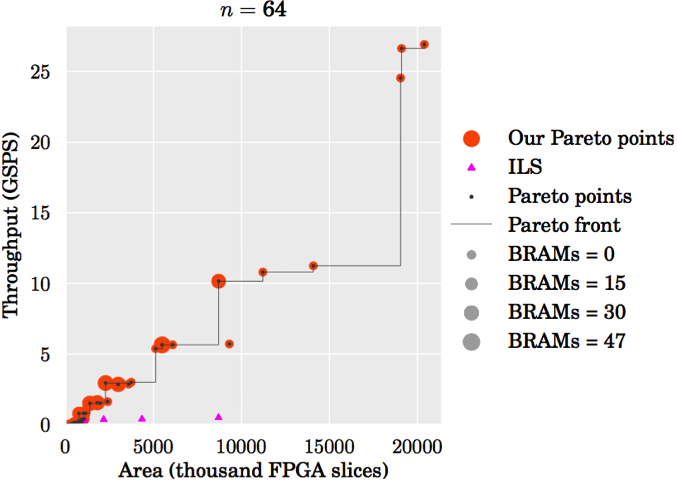
Design space. The plots below show an evaluation of the design space for the sizes n = 16, 256, 2048. All designs that fit onto the target FPGA (Xilinx Virtex-6 XC6VLX760) are shown. In each plot, the x-axis is the number of FPGA slices used, the y-axis the throughput in Giga samples per second, and the size of the marker is proportional to the number of BRAMs used. Plot (c) zooms into a small region of plot (b). Pareto-optimal designs are connected by a line. The smallest Pareto-optimal design in all cases is obtained with SN5, maximum iterative reuse and minimum streaming width (2). For comparison purposes, we added to our design space an implementation of a linear sorter, as described in [4, pp. 5]. Linear sorters input one element at the time, sorting them into a register array as they are received.
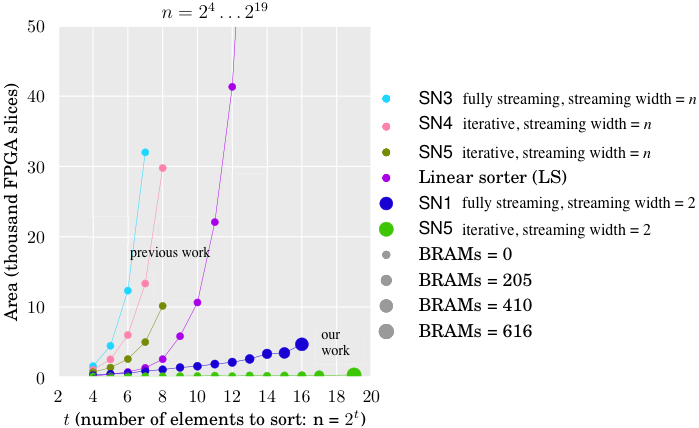
Comparison to prior work. To the best of our knowledge, we generate the first designs for sorting networks with streaming reuse to dramatically reduce area cost, even for high throughput designs. This is illustrated in the figure below, which shows the area cost (y-axis) of various sorters for increasing n (x-axis) that fit onto the target FPGA. With prior work it was possible to build the designs of the four uppermost lines [4,8,9]. Our work enables, for example, the two bottom lines: fully streaming designs (SN1 fully streaming with streaming width 2) and a design with maximal reuse (SN5 iterative with streaming width 2), i.e., it uses only one configurable 2-input sorter. Both designs require more BRAM but considerably less slices. Even a sorter for 219 elements can be fit onto the target FPGA.
References
- Marcela Zuluaga, Peter A. Milder and Markus Püschel
Streaming Sorting Networks
ACM Transactions on Design Automation of Electronic Systems, Vol. 21, No. 4, pp. 55, 2016
- Marcela Zuluaga, Peter A. Milder and Markus Püschel
Computer Generation of Streaming Sorting Networks
Proc. Design Automation Conference (DAC), pp. 1245-1253, 2012 - Peter A. Milder, Franz Franchetti, James C. Hoe and Markus Püschel
Formal Datapath Representation and Manipulation for Implementing DSP Transforms
Proc. Design Automation Conference (DAC), pp. 385-390, 2008 - Franz Franchetti, Frédéric de Mesmay, Daniel McFarlin and Markus Püschel
Operator Language: A Program Generation Framework for Fast Kernels
Proc. IFIP Working Conference on Domain Specific Languages (DSL WC), 2009 - Kenneth E. Batcher
Sorting Networks and their Applications
Spring Joint Computer Conference (AFIPS), 1968 - Donald Knuth
The Art of Computer Programming: Sorting and Searching
Addison-Wesley Pub. Co., 1968 - Markus Püschel, Peter A. Milder, and James C. Hoe
Permuting Streaming Data Using RAMs
Journal of the ACM, 26(2), 2009 - Peter A. Milder, James C. Hoe, and Markus Püschel
Automatic Generation of Streaming Datapaths for Arbitrary Fixed Permutations
Proc. Design, Automation and Test in Europe (DATE), 2009 - Christophe Layer, Daniel Schaupp, and Hans-Jörg Pfleiderer
Area and Throughput Aware Comparator Networks Optimization for Parallel Data Processing on FPGA
Proc. Symposium Circuits and Systems (ISCAS), 2007 - Harold S. Stone
Parallel Processing with the Perfect Shuffle
IEEE Transactions on Computers, 1971 - Jorge Ortiz and David Andrews
A Configurable High-throughput Linear Sorter System
Proc. International Symposium on Parallel Distributed Processing (IPDPSW), 2010
More publications on IP cores for FPGAs/ASICs
Online software generator for the discrete/fast Fourier transform
Copyrights to many of the above papers are held by the publishers. The attached PDF files are preprints. It is understood that all persons copying this information will adhere to the terms and constraints invoked by each author's copyright. These works may not be reposted without the explicit permission of the copyright holder. Some links to papers above connect to IEEE Xplore with permission from IEEE, and viewers must follow all of IEEE's copyright policies.
More information
Contact: Marcela Zuluaga, [first].[last] AT inf.ethz.ch
Copyright (c) 2012 Marcela Zuluaga for the Spiral Project, ETH Zurich, Switzerland
