Multiplexed Multiplier Block Generator

Explanation

The problem of multiplying by a given set of constants based on a control input has been studied to a much lesser degree in the literature than parallel multiplier blocks. One major difference to the parallel multiplier blocks is that now multiplexers are needed, which, as the add/subtracts have area requirements. We have developed a tool that generates multiplexed multiplier blocks for any set of constants and bitwidth. Below we show a general multiplexed multiplier block and a very simple example - a multiplier block for the multiplexed multiplication with the constants 11 and 21, generated by our tool.

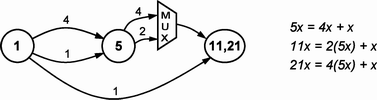Multiplexed multiple constant multiplication (MUXMCM)	An example multiplier block, implementing multiplication by 11 and 21

Other multiplierless problems

Generator

Input: A list of integer or fixed-point constants c_1, ...,c_n.

Output: Synthesizable Verilog code and the corresponding directed acyclic graph (DAG) for the multiplier block implementing the time-multiplexed multiplications c_i*x for i=1..n. The only operations used in the generated DAG and code are additions, subtractions, multiplexers and shifts.

Parameter	Value	Explanation
Constants	0.2303778133088 0.7148465705529 0.6308807679298 0.0279837694168 0.1870348117190 0.0308413818355 0.0328830116668 0.0105974017850	Positive integer or floating point constants. Maximum 20 constants. Floating point constants will be converted into integers using the number of fractional bits given below. Maximum 20 bits after conversion.
Fractional bits	0 (integer constants)    123 456 78 91011 121314 151617 181920	Constants will be scaled by 2^f, where f is the value given here. Use 0 for integer constants.
Input bits	123 456 78 91011 121314 151617 181920 212223 242526272829303132	The circuit's input bitwidth

Benchmark

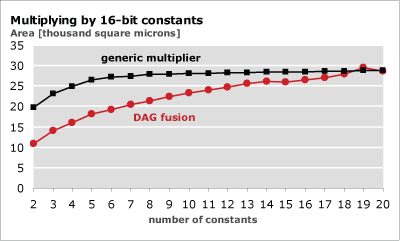
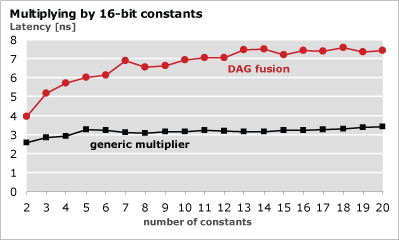
The Figures below show an example benchmark from [1]. It is a comparision between a baseline approach consisting of a generic multiplier and a lookup table, and the above presented dag fusion algorithm. Each point in the plots is averaged over 10 sets of randomly drawn 16 bit constants. Considerable area gains, compared to the multiplier based solution, are possible at the cost of increased latency. In the example below, for up to 18 constants our multiplier blocks use less resources than the baseline approach, despite double the latency.

Number of constants versus area for 16-bit constants	Number of constants versus latency for 16-bit constants

Software Download

Our software is available under GNU GPL license. A commercial license can be obtained on request.

muxmcmtool.zip (3.5 MB)

References

1. Peter Tummeltshammer, James C. Hoe and Markus Püschel
   Time-Multiplexed Multiple Constant Multiplication
   IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, Vol. 26, No. 9, pp. 1551-1563, 2007


2. Peter Tummeltshammer, James C. Hoe and Markus Püschel
   Multiple Constant Multiplication By Time-Multiplexed Mapping of Addition Chains
   Proc. Design Automation Conference (DAC), pp. 826-829, 2004

Copyrights to many of the above papers are held by the publishers. The attached PDF files are preprints. It is understood that all persons copying this information will adhere to the terms and constraints invoked by each author's copyright. These works may not be reposted without the explicit permission of the copyright holder. Some links to papers above connect to IEEE Xplore with permission from IEEE, and viewers must follow all of IEEE's copyright policies.

More information

Copyright (c) 2006 by Peter Tummeltshammer for the SPIRAL Project, Carnegie Mellon University

Contact: Peter Tummeltshammer, petertu AT ecs DOT tuwien DOT ac DOT at