SPIRAL Backprojection Package
What is it?
An efficient, flexible C package for computing the fast hierarchical backprojection. The package has the following features:- Recursion method without downsampling (no cost savings);
- Recursion with downsampling (cost savings, the actually fast backprojection algorithm);
- Direct backprojection (cubic cost);
- Choice of interpolators including, next-neighbor, linear, cubic, cubic spline, and sinc interpolator.
Overview
The backprojection operation arises from a formula for inverting the Radon transform. It is used in popular image reconstruction algorithms for computed tomography (CT), spotlight-mode synthetic aperture radar (SAR), and other imaging techniques. All these techniques have one thing in common: the acquired data represents, either directly or after some preprocessing, the Radon transform of the scanned image---a collection of image projections at various angles.
The image reconstruction problem, thus, equals the problem of inverting the Radon transform. The most notable reconstruction methods are Fourier-based techniques that rely on the slice-projection property of the Radon transform, and widely used filtered backprojection (FBP) algorithms.
In the FBP approach, each of the projections in the Radon transform is filtered with a windowed ramp filter and then backprojected to reconstruct the image. The backprojection is the costliest stage of the reconstruction with O(N^3) operations, N being the image size in pixels, whereas Fourier techniques require only O(N^2 log N) operations. Efficient implementation of the backprojection operation is therefore crucial for the overall performance of the algorithm.
The fast hierarchical backprojection algorithm (FHBP) [1] reduces the cost of the backprojection asymptotically to O(N^2 log N) by dividing the problem into smaller problems that require fewer projections for effective reconstruction. We provide a flexible C package that implements different variants of the FHBP algorithm, including the direct O(N^3) backprojection as a special case. The software allows the user to choose parameters that control the depth of the recursion, the amount of oversampling, and the choice of the interpolating function, all designed to exploit possible runtime/distortion tradeoffs.
[1] S. Basu and Y. Bresler, "O(N^2 log_2(N)) filtered backprojection reconstruction algorithm for tomography,'' IEEE Trans. on Image Processing, vol. 9, pp. 1760--1772, October 2000.
Benchmarks
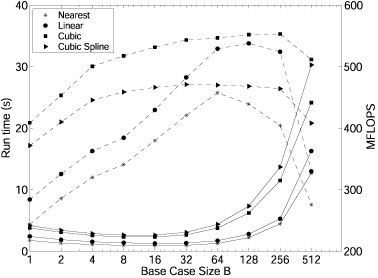 |
Runtime and Performance in MFLOPS for different levels of recursion in the fast backprojection. The fastest runtime is obtained when recursing only up to image size 16 x 16 and to continue then with the direct backprojection. For this strategy, we achieve ~500 MFLOPS, about 15% of the peak performance (excluding vector instructions.
See the paper below for more experimental results. |
Download
The most recent version of the fast backprojection package is available for download (37 KB) including a commented sample input file and an uncommented sample input file.References
- Thammanit Pipatsrisawat, Aca Gacic, Franz Franchetti, Markus Püschel and José M. F. Moura
Performance Analysis of the Filtered Backprojection Image Reconstruction Algorithms
Proc. International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Vol. 5, pp. 153-156, 2005
Copyrights to many of the above papers are held by the publishers. The attached PDF files are preprints. It is understood that all persons copying this information will adhere to the terms and constraints invoked by each author's copyright. These works may not be reposted without the explicit permission of the copyright holder. Some links to papers above connect to IEEE Xplore with permission from IEEE, and viewers must follow all of IEEE's copyright policies.
