Program Generation for the All-Pairs Shortest Path Problem
What is it?
A program generator for the all-pairs shortest paths problem (APSP) based on the Floyd-Warshall algorithm. For a given problem size, the generator automatically generates and times programs with different degrees of blocking and loop unrolling to find the fasest for a givne platform. The generator can output standard scalar C code as well as SSE SIMD vector code. The design of the generator is in spirit similar to ATLAS.
Overview
The all-pairs shortest path problem (APSP) finds the length of the shortest path for all source-destination pairs in a (positively) weighted graph. It belongs to the most fundamental problems in graph theory. The problem occurs in many algorithms in communication, networking, and circuit design.
The APSP is solved by the well-known Floyd-Warshall (FW) algorithm, which computes the solution inplace from the weight matrix of the graph using a triple loop similar to MMM, but involving only additions and minimum operations, and with dependencies that restrict the ordering of the three loops (the k-loop has to be the outermost one). To optimize cache performance, [1] introduced a tiled version of the FW algorithm. Further improvements were made in [2], which showed that the tiling can be done recursively up to some chosen base case and combined with a ZMorton data layout to increase performance.
Our program generator [3] goes beyond the above approaches. First, it is a program generator, not a library. Further, we 1) consider different levels and degrees of blocking; 2) different degrees of unrolling; and 3) generate scalar as well as SIMD vector code for data type float and integer.
We are faster than other approaches and achieve considerable performance as shown below.
Benchmarks
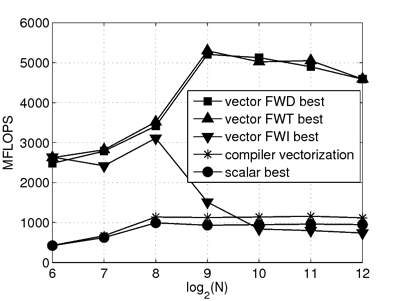 |
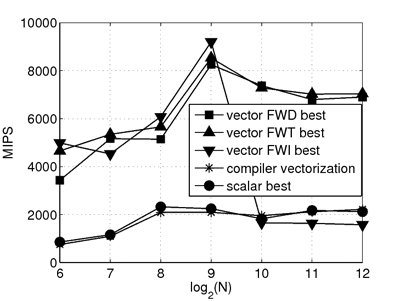 |
| Performance obtained on a Pentium 4, data type single precision float. Vector means 4-way SSE. | Performance obtained on a Pentium 4, data type short integer. Vector means 8-way SSE. |
Benchmarks on a 3.6 GHz (model number 560), with 16 KB L1 cache, 1MB L2 cache, and 1 GB main memory. All algorithms (FWD, FWT, FWI) are variants of Floyd-Warshall. y-axis: performance, x-axis: base-2 log of problem size (number of nodes in graph). The best performance is achieved in both cases (left: float; right: short integer) with FWD and FWT. More details in [3].
References
- G. Venkataraman, S. Sahni, and S. Mukhopadhyaya
A blocked all-pairs shortest-paths algorithm
J. Experimental Algorithms, 8:2.2, 2003 - J.-S. Park, M. Penner, and V. K. Prasanna
Optimizing graph algorithms for improved cache performance
IEEE Transactions on Parallel and Distributed Systems, 15(9):769–782, 2004 - Sung-Chul Han, Franz Franchetti and Markus Püschel
Program Generation for the All-Pairs Shortest Path Problem
Proc. Parallel Architectures and Compilation Techniques (PACT) , pp. 222-232, 2006
Copyrights to many of the above papers are held by the publishers. The attached PDF files are preprints. It is understood that all persons copying this information will adhere to the terms and constraints invoked by each author's copyright. These works may not be reposted without the explicit permission of the copyright holder. Some links to papers above connect to IEEE Xplore with permission from IEEE, and viewers must follow all of IEEE's copyright policies.
More Information
Contact: Sungchul Han, sungchul_han (at) xxxsamsung.com (delete xxx)
