Optimized Sparse Fast Fourier Transform
What is it?
The Sparse Fast Fourier Transform is a recent algorithm developed by Hassanieh et al. [2, 3] for computing the the discrete Fourier Transforms on signals with a sparse (exact or approximately) frequency domain. The algorithm improves the asymptotic runtime compared to the prior methods based on pruning (e.g., [4]).
A reference implementation of the SFFT exists on the SFFT website at MIT proves that the algorithm can be faster than modern FFT libraries. However, the reference implementation is not optimized for modern hardware features such as the cache hierarchy, vector instruction sets, or multithreading.
We have analyzed the performance of the reference implementation and performed several optimizations [1]. The resulting code is two to five times faster than the original and provided below.
Benchmarks
Here are a few example benchmarks. The complete set can be found in the Master thesis below.
 |
 |
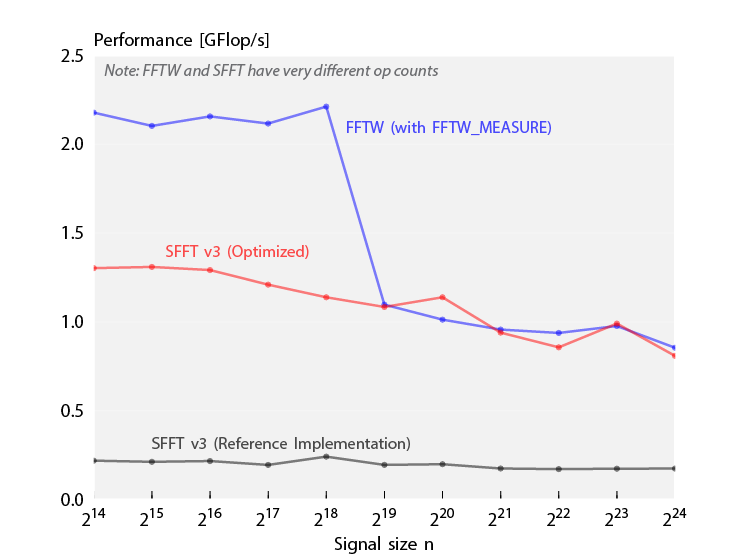
The graphic shows a comparison of the SFFT v3 reference implementation, the optimized SFFT v3 implementation and FFTW, with respect to implementation efficiency. The SFFT performance was increased significantly by applying different optimizations and is now about equally efficient as the high- performance FFTW library for large input sizes. |
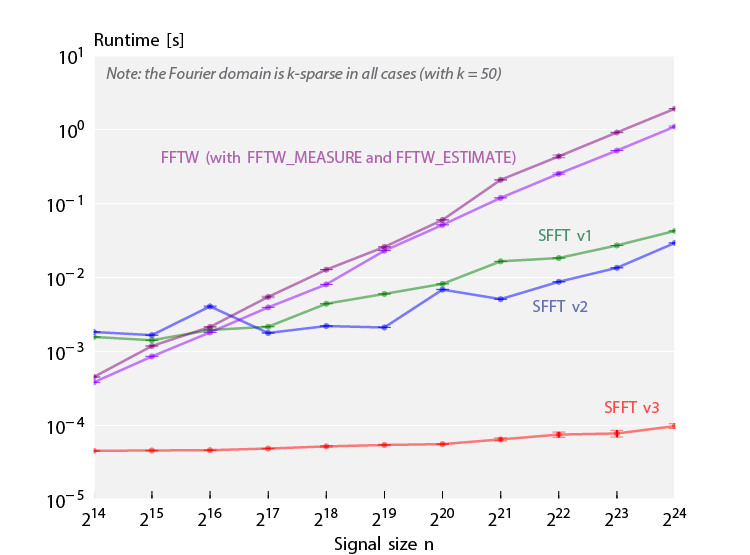
A runtime benchmark comparing the three SFFT versions and FFTW (with the two optimization levels FFTW_ESTIMATE and FFTW_MEASURE). The number of nonzero Fourier coefficients was set to k=50. The SFFT implementations are in almost all cases faster than the FFTs; especially version 3 outperforms the other algorithms for all input sizes. Also note that the SFFT's asymptotic runtimes are not linear in the signal size as in the FFTs; thus, the SFFT runtimes increase slower. |
 |
 |
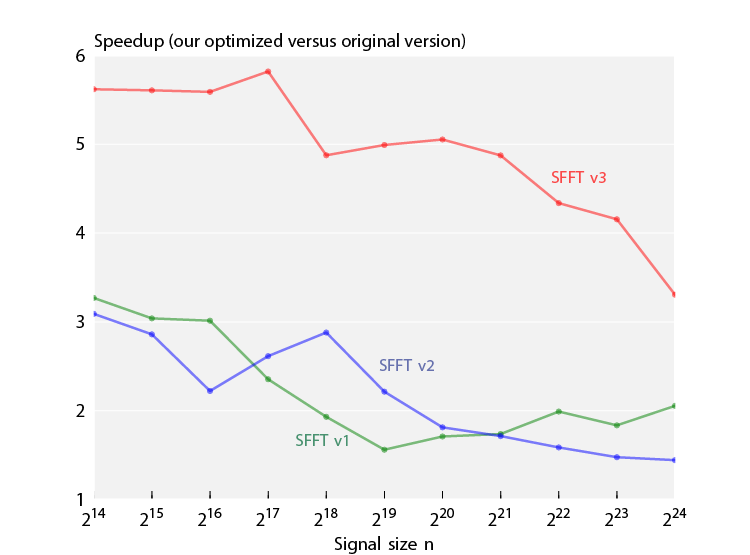
The plot shows speedups of the different optimized SFFT versions compared to their reference implementations. It shows that the most gain was achieved in SFFT v3. The maximum speedup is above 5. For example, a SFFT v3 run with parameters n=2^16 and k=50 would be 5 times faster with the optimized implementation than with the reference implementation. |
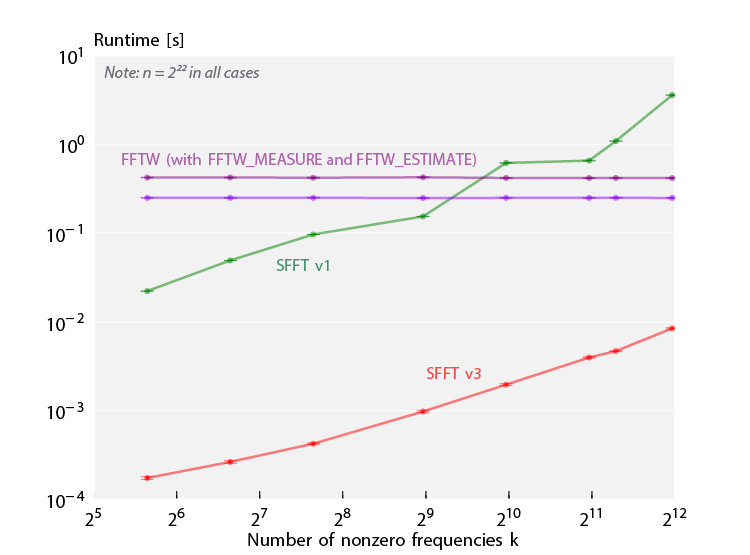
A runtime benchmark comparing SFFT v1, v3 and FFTW. This time, the signal size n was kept constant to n=2^22, and the number of nonzero Fourier coefficients k was varied. Since the FFT's runtime does only depend on the signal size, it is constant. SFFT v3 is faster than the FFTW runs over the whole range of the experiment; SFFT v1 is faster than FFTW up to k=2^9. |
Download
The original reference implementation can be downloaded at the SFFT website at MIT. The inventors of the SFFT have generously provided us with a prototype of the code for exact sparse case (version 3), which is included in the optimized version. The optimized code has the same constraints as the original and is distributed under a GNU public license.
sfft-0.1.0.zip (456 KB)
sfft doc (html)
sfft documentation (pdf, 120 KB)
References
- Jörn Schumacher and Markus Püschel
High-performance sparse fast Fourier transforms
Proc. IEEE Workshop on Signal Processing Systems (SIPS), pp. 1-6, 2014 - Jörn Schumacher
High Performance Sparse Fast Fourier Transform
Master thesis, Computer Science, ETH Zurich, Switzerland, 2013 - Haitham Hassanieh, Piotr Indyk, Dina Katabi, and Eric Price
Simple and Practical Algorithm for Sparse Fourier Transform
Proc. Symposium on Discrete Algorithms (SODA), pp. 1183-1194, 2012 - Haitham Hassanieh, Piotr Indyk, Dina Katabi, and Eric Price
Nearly Optimal Sparse Fourier Transform
Proc. Symposium on Theory of Computing (STOC), pp. 563-578, 2012 - Franz Franchetti and Markus Püschel
Generating High-Performance Pruned FFT Implementations
Proc. International Conference on Acoustics, Speech, and Signal Processing (ICASSP), pp. 549-552, 2009
Note: for [2, 3] a preprint can be downloaded here.
Copyrights to many of the above papers are held by the publishers. The attached PDF files are preprints. It is understood that all persons copying this information will adhere to the terms and constraints invoked by each author's copyright. These works may not be reposted without the explicit permission of the copyright holder. Some links to papers above connect to IEEE Xplore with permission from IEEE, and viewers must follow all of IEEE's copyright policies.
